Sequential Ejection
2024 July 15 at 20:46
Often, a programmer will be faced with a sequence of data from which only certain elements should be retained for further processing. For example, in a game, one might have a list of entities and wish to keep only those that are alive and within the loading zone. Or in a text processing task, one might wish to select only records which begin with a valid date (per ISO 8601) within the past year. This is called a “filter” or “select” operation. We will walk through a few different ways that one might implement this, and discuss the implications of each. The example code is written in the C programming language, because it cleanly distinguishes data from references to that data. However, the data structures used here are not intended to be generically applicable.
First, let us lay down some base assumptions. The data exists in memory as an ordered sequence. The original, unfiltered data will not be needed later; in other words, in-place operation is allowed. Certainly an out-of-place filter that preserves the original data can run in linear time and auxiliary space, at least when the sequence is composed of references or other cheaply copied types. We explore the question of how efficient the operation can be when allowed to overwrite the original data. The examples here will use a sequence of integers.
The target that we will eventually reach is as follows.
void filter(_Bool(*is_valid)(int), struct IntArray *arr) {size_t next_free = 0;for (size_t i = 0; i < arr->size; i++) {if (!is_valid(arr->data[i])) continue;arr->data[next_free] = arr->data[i];next_free += 1;}arr->size = next_free;}
Linked-List Input
For this section, and only this section, we’ll assume that the input is given as a linked list. The list structure will be as follows:
struct IntList {struct IntList *tail;int value;};
That is, given a node-pointer n,
the next node is n->tail
and the contained data is n->value.
An empty list is NULL.
The intended signature for our filter function is as follows:
struct IntList *filter(_Bool(*is_valid)(int), struct IntList *head);This declares the function “filter”
to take two arguments.
The first is a function is_valid
that maps a data point (the int)
to a Boolean value (the _Bool)
that represents whether the value should be retained (true)
or discarded (false).
The second argument is the head of the list.
Finally, our function must return a new head-pointer,
in case some initial elements are discarded.
Linked lists do not support efficient random access, so a good solution will read the list in one linear stream. We will maintain a pointer to the previous link-point, be that the list head or the tail field of the most recently retained node. At each node, we test whether it is valid. If the data is valid and should be retained, then the link-point is updated and we advance to the next node. Otherwise, we create a link from the link point to the current node’s tail, thereby removing the current node from the structure, and then free the current node.
#include <stdlib.h>struct IntList *filter(_Bool(*is_valid)(int), struct IntList *head) {struct IntList **link_point = &head;struct IntList *current = head;while (current) {if (is_valid(current->value)) {link_point = &(current->tail);} else {*link_point = current->tail;free(current);}current = *link_point;}return head;}
Suppose, for example, that we have a linked list of four elements, and we wish to retain the second and fourth. The algorithm proceeds as depicted below, streaming through the list in a single pass and freeing unnecessary elements as it goes. This runs in Θ(n) time for a list of n elements, using only two pointers’ worth of auxiliary space.
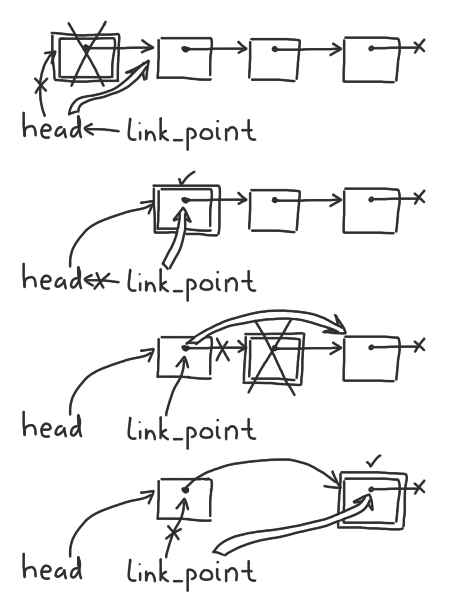
The operation of the above algorithm. At each step, the current node is boxed. Nodes and links that are deleted are shown crossed out, and newly created links are shown as a distinct wide kind of arrow.
Naïve Application to Arrays
From this point, we assume that the input is not a linked list but a dynamic array. Arrays use contiguous storage to offer efficient random access, but the flipside of this is that the insertion or removal of an interior element requires shifting the later elements around. The dynamic array structure used for the remainder of this article is as follows:
#include <stddef.h>struct IntArray {int *data;size_t size;size_t capacity;};
For the sake of clarity, in-place array-based filter procedures will not return output. All modifications are contained within the array, and the outer structure need not ever change. After this change of return type and a suitable change of argument type, we can define a new filter.
void filter(_Bool(*is_valid)(int), struct IntArray *arr) {for (size_t i = 0; i < arr->size; i++) {if (is_valid(arr->data[i])) continue;for (size_t j = i+1; j < arr->size; j++) {arr->data[j-1] = arr->data[j];}arr->size -= 1;i -= 1;}}
Here, every removal requires that all later elements be moved down. Notice that the loop counter is also decremented in this situation, as the next element is moved into the current location. When the loop counter updates again, it will return to examine that next element.
If no element is retained, then the first removal will move n−1 elements, the second will remove n−2 elements, and so on, until eventually no elements remain to be moved. In other words, the number of copies is the sum of the first n natural numbers. Although we still maintain only a constant number of auxiliary pointers, the time complexity is now Θ(n2).
Next, we explore two ways to get back the good time-complexity of the linked-list implementation.
Saving Time Through Shuffling
The first attempt at filtering arrays directly mirrored the linked-list implementation. This means that we took on the cost of keeping data contiguous, but did not take advantage of the random-access potential of arrays. If the order of the data is not important, then changing the arrangement can improve runtime significantly by moving exactly one element per removal.
void filter(_Bool(*is_valid)(int), struct IntArray *arr) {for (size_t i = 0; i < arr->size; i++) {if (is_valid(arr->data[i])) continue;arr->data[i] = arr->data[arr->size - 1];arr->size -= 1;i -= 1;}}
The difference between this and the naïve port
is that instead of copying the entire remaining array,
only the final element is moved.
Again, this should only be used when the order of the data
is immaterial to subsequent operations,
as the order is not stable.
If the input array contains the natural numbers from 1 to 10,
in order, and even numbers are retained,
then the output is {10,2,8,4,6}.
On the other hand, this is a simple way to return to the Θ(n) time-complexity without incurring any additional space-complexity.
Stable, Small, and Speedy
The previous array-based filters leave retained elements in-place, and they remove elements by moving one or more unchecked elements into their place. If instead it is the retained elements that move, then we can get all of the desired properties at once.
void filter(_Bool(*is_valid)(int), struct IntArray *arr) {size_t next_free = 0;for (size_t i = 0; i < arr->size; i++) {if (!is_valid(arr->data[i])) continue;arr->data[next_free] = arr->data[i];next_free += 1;}arr->size = next_free;}
Retained elements are moved over earlier discarded elements, until the input stream is exhausted. The size is changed one time, at the end. As this algorithm proceeds via a single stream, it has a Θ(n) time-complexity and still requires only a constant number of auxiliary pointers. As the retained elements are condensed but not reordered, the resulting filter is stable. This is the best choice.